Redistricting: A Modest Proposal

The problem:

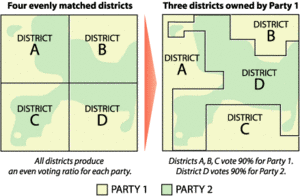The party in power in a state (legislature and governor), using state-of-the-art software, gets to redraw the state's U.S. Congressional districts to maximize the number of Congressional seats its party members win. They do it so effectively, concentrating the votes of their enemies and spreading theirs out evenly, that in the last Congressional elections, only 4 out of 435 incumbents were defeated. (There is an excellent Wikipedia article giving more background; I'm using the graphics from that article, with permission of the Wikipedia.)

This isn't democratic. If this system were in operation in another country, we would not call their elections "free and fair." Why should Americans have less democracy than, say, Iraqis?

The proposed solution:

Hire retired judges, or other "non-partisan" officials, to draw the district boundaries, rather than leaving it to the winners of the state elections.

The problem with the proposed solution:

Who's non-partisan? Really. C'mon.

An Observation

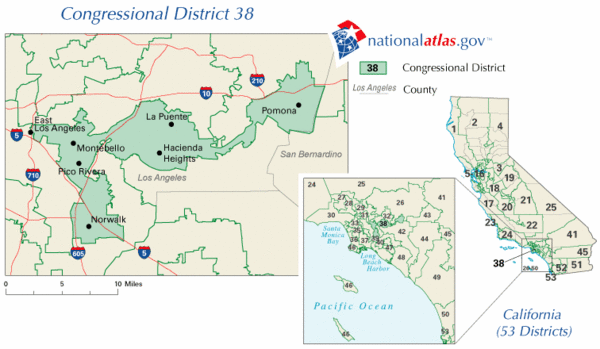
Gerrymandering is only possible because districts can be drawn in any shape whatsoever so long as the districts don't cross state boundaries. I've seen districts that run down the middle of a major street (where no one lives) just so that they can snag a small pocket of voters down the road. The graphic is of Grace Flores' minority-majority district. It guarantees Democrat Grace Flores a district at the expense of Democrats in all the adjacent districts.

My Modest Proposal

Require all congressional districts to be convex and stout.

Convexity: No district may be more than 10% smaller in area than the smallest convex polygon that can be drawn around its boundaries; except that any area of such convex polygon falling outside the boundaries of the state shall not count for this calculation.

Draw any number of straight lines around the district. If more than 10% of the area of the resulting shape isn't inside the district, the district is no good and must be redrawn. The 10% allows for streams and mountains. Not that modern gerrymandered districts pay much attention to rivers and mountains. Obviously, where states are concave, the districts must be, too.

Stoutness: No district may be drawn such that the longest distance between any two points on its boundary, with the exception of points falling on the state boundary, is more than two and a half times as long as the shortest line that can be drawn that bisects the district.

Districts can't be too narrow. Draw the shortest possible line that divides the district in half. The district can't be more than three times as long in any direction as this line. Points on the state borders don't count because some states have long, narrow "panhandles," and it is impossible to draw stout districts there. Note that even in a square, the longest distance between two points on its boundary is 1.4 times the shortest distance that bisects the square.

These two simple geometrical rules would not eliminate the impulse to gerrymander. But they would drastically reduce the gerrymanderers' flexibility; and flexibility is the key to corrupt redistricting. The beauty of using geometry is that geometry cannot be made to lie. It is hard to prove a district is "unfair." It is easy to prove that a district is concave.

Thoughts? Email me at craftyscreenwriting at gmail dot com.

---